变换物体与变换坐标系
在2D中的例子“将一个物体顺时针旋转20度”。变换物体(这里是旋转),意味着旋转物体上所有的点。这些点被移动到一个新位置,使用同一坐标系来描述变换前和变换后点的位置。
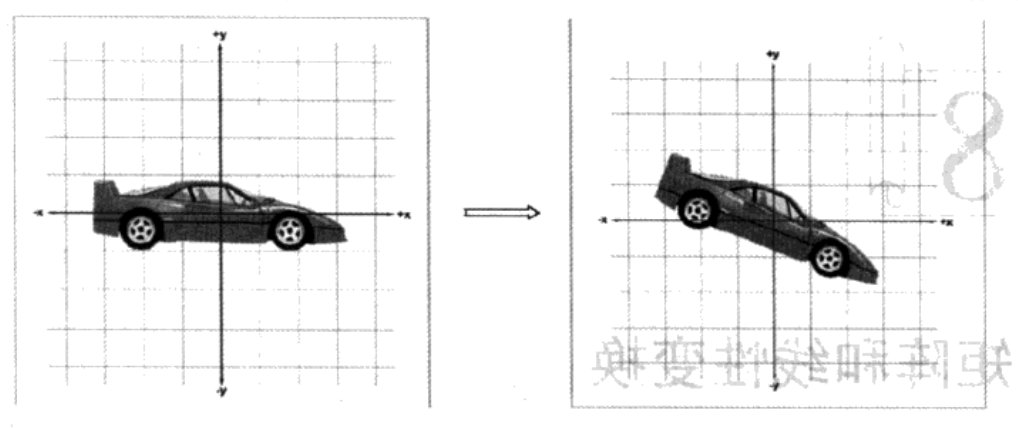
顺时针将物体旋转\(20^{\circ}\)
现在,和变换坐标系的概念进行比较。旋转坐标系后时,物体上的点实际没有移动,我们只是在另外一个坐标系中描述它的位置而已。
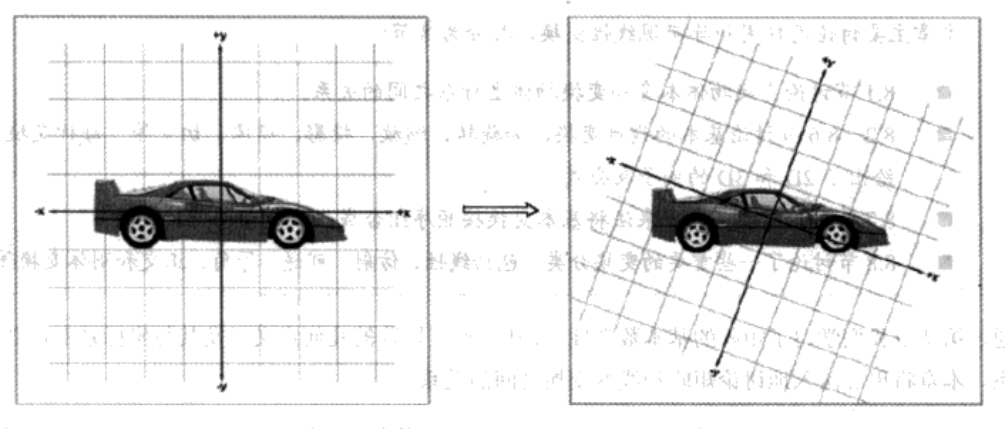
顺时针旋转坐标系\(20^{\circ}\)
这两种变换在某种意义上是等价的,现在,先看看它们各自的做优点。
变换物体的用处非常明显。例如,为了渲染一辆车,必须将点从车的物体坐标系变换到世界坐标系,接着到摄像机坐标系。
那么,为什么还要变换坐标系呢?
其实旋转坐标系能起到很好的作用。
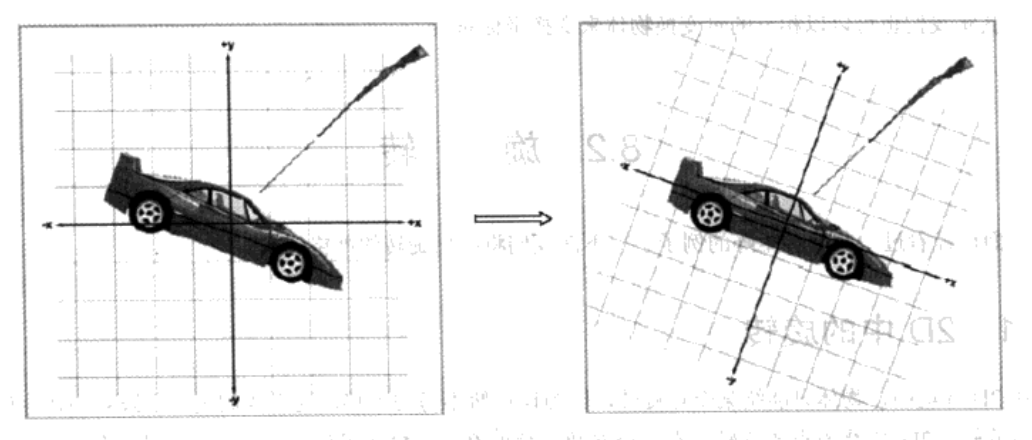
旋转坐标系的盒子
上图展示了一把枪,正向汽车发射子弹。我们一开始就知道世界坐标系中枪的位置和子弹的弹道。现在,想象一下世界坐标系被旋转到和车的物体坐标系重合的位置,而与此同时保持车、枪、子弹的弹道不动。这样,我们得到了枪和子弹弹道在车的物体坐标系中的坐标,接着就可以作碰撞检测以检查子弹是否会击中汽车了。
当然,也可以将车旋转到世界坐标系,在世界坐标系中作碰撞检测,但这要花费更多的时间,因为车的模型可能有大量的顶点和三角形,计算量太大。现在,不用担心实际变换的细节问题,这正是下面要解释的。
可以变换物体,也可以变换坐标系,某些情况下一种方法比另一种更合适。
对这两种变换保持一种概念上的区别还是有必要的,有些情况下需要进行物体变换,另外一些情况下则需要进行坐标系的变换。然而,这两种变换实际上是等价的,将物体变换一个量等价于将坐标系变换一个相反的量。
如下图右边的那幅图显示出坐标系沿顺时针方向旋转了\(20^{\circ}\)。现在,旋转整个图(坐标系和车),使坐标系指向回到标准。因为旋转的是整个图,所以仅仅相当于换了一个角度来看这张图,没有改变车和坐标系的相对位置。
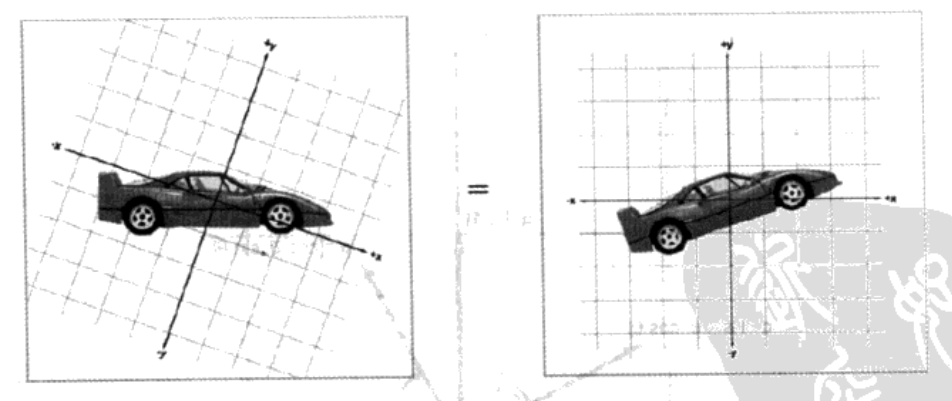
旋转坐标系相当于以相反的量旋转物体
变换物体相当于以相反的量变换描述这个物体的坐标系。
当有多个变换时,则需要以相反的顺序变换相反的量。
旋转
2D中的旋转
在2D环境中,物体只能绕某个点旋转,因为现在暂不考虑平移,这里我们进一步限制物体,使其只绕原点旋转。2D中绕原点的旋转只有一个参数:角度\(\theta\),它描述了旋转量。逆时针旋转经常(不是必须)被认为是正方向,顺时针方向是负方向。
下图展示了基向量\(p, q\)绕原点旋转,等到新的基向量\({p}', {q}'\)。
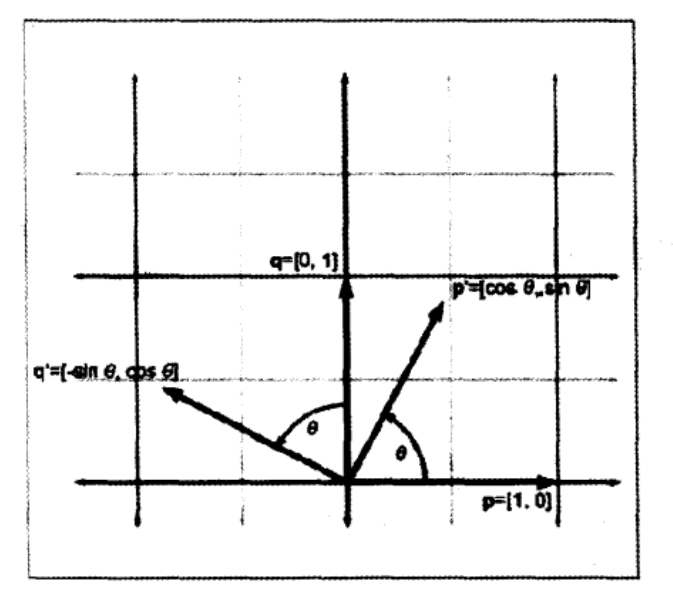
绕2D中的原点旋转
知道旋转后基向量的值,就可以用下列公式构造矩阵:
\[R\left( \theta \right) = \left[ \dfrac {p'} {q'}\right] = \begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos \theta \end{bmatrix}\]2D旋转矩阵